
来源:赛斯拜克 发表时间:2023-10-11 浏览量:390 作者:awei
高光谱相机波段选择是高光谱遥感技术应用中的重要问题,它直接影响到图像采集的质量和精度。本文将介绍高光谱相机波段选择的基本原则和考虑因素,以及常用的波段范围和对应的实际应用场景。
高光谱相机波段选择是高光谱遥感技术应用中的重要问题,它直接影响到图像采集的质量和精度。本文将介绍高光谱
相机波段选择的基本原则和考虑因素,以及常用的波段范围和对应的实际应用场景。

高光谱相机波段选择应遵循以下几个原则:
1. 针对性原则:针对不同的应用领域和目标,需要选择不同的波段范围。例如,在地质遥感领域,需要关注可见光-近
红外波段;在环境监测领域,需要关注中红外-长波红外波段。
2. 宽波段原则:为了获得更多的光谱信息,应尽可能选择较宽的波段范围。一般来说,波段范围越宽,获取的光谱信息
越丰富。
3. 分辨率原则:在满足宽波段原则的前提下,应尽量选择具有较高空间分辨率的波段。高空间分辨率可以更好地揭示地
物细节和空间结构信息。
4. 稳定性原则:选择的波段应具有较好的稳定性和抗干扰能力。例如,应避免选择容易受到大气吸收和散射干扰的波段。
5. 经济性原则:在满足前四个原则的前提下,应尽量选择成本较低的波段范围。
1. 可见光-近红外波段(400-1000nm):该波段范围是地物反射率最高的波段,适合于地物分类、植被覆盖度监测、土
地利用/土地覆盖图斑提取等应用场景。常用的商业高光谱相机如美国宇航局(NASA)的AIS2和AIS3,以及以色列Visi
onMap公司的VisH烟火探测相机等均包含该波段范围。
2. 短波红外波段(1000-2500nm):该波段范围是地物透射率最高的波段,适合于透过植被探测地下目标、水体污染监
测、大气气体成分遥测等应用场景。常用的商业高光谱相机如美国宇航局的AIS5/AIS6、以色列VisionMap公司的VisSWIR
等均包含该波段范围。
3. 中红外-长波红外波段(2500-10000nm):该波段范围是地物发射率最高的波段,适合于地物热辐射特性遥感、地物
识别与分类、水体和大气温度监测等应用场景。常用的商业高光谱相机如美国宇航局的FLIR、德国制冷公司的HRR等均包
含该波段范围。
4. 超宽带波段(<10nm):该波段范围是具有超宽带特性的高光谱成像系统的工作范围,适合于超宽带通信、雷达成像、
高精度导航等应用场景。常用的商业高光谱相机如美国宇航局的HCONS、芬兰Spectral Imaging公司的i-SPEED等均包含
该波段范围。
高光谱相机波段选择应根据实际需求和应用领域进行综合考虑,选择合适的波段范围,以获得更好的应用效果。
高光谱遥感图像波段选择采用的策略主要包括:
(1)以评价准则为依据的波段选择
(2)以特征选择方式为依据的波段选择
(3)以训练样本为依据的波段选择
(4)以与应用模型的关系为依据的波段选择
一、以评价准则为依据的波段选择
从波段选择采用的评价准则来看,高光谱遥感图像的波段选择方案包括:
(1)以信息量作为波段选择的标准,选择信息总量最大的波段子集,通常采用信息熵、互信息、交叉熵、联合信息熵、信息散度、方差、协方差矩阵特征值等来构建信息量的评价指标。需要注意的是,噪声对基于信息论的这些指标的影响较大,噪声大的波段会导致较大的方差,同时也会降低与其他波段的相关性而被误选,但这些受到噪声或者异常影响的波段往往具有较低的鲁棒性和可靠性。
(2)以类别可分性作为波段选择标准,期望选取的波段子集有利于研究地物的分类识别。衡量类间可分性大小常以距离来度量,典型的度量指标有离散度、B距离(Bhattacharyya distance)、JM距离(Jeffreys Matusita distance)等。
以波段间的相关度作为波段选择的标准,选择相关性最弱的波段子集,以减小信息冗余,常用光谱相关系数、光谱角、光谱信息散度和正交投影散度等作为度量指标。
二、以特征选择方式为依据的波段选择
本研究所用遥感数据以谷歌地球引擎(GEE)为分析平台。这是由谷歌、卡内基梅隆大学和美国地质调查局联合开发的基于云计算的地理信息处理系统。此平台提供了大量影像数据,通过依靠Google的高性能集群服务器对影像进行在线可视化处理,信息提取十分快捷。本研究所用的卫星数据源为陆地卫星地表反射率数据(LSR)系列数据和哨兵二号多光谱2a级数据集。
LSR系列数据包含陆地卫星专题制图仪(TM)、陆地卫星增强型专题制图仪(ETM+)、陆地卫星陆地成像仪(OLI)影像,时间分辨率为16d,空间分辨率为30m,均包含3个可见光波段及一个近红外波段。LSR数据产品是通过陆地卫星生态系统扰动自适应处理系统(LEDAPS)处理,利用大气表观反射率(TOA)和亮温(BT)数据,对太阳光谱辐射传输模型(6S)中的卫星信号进行二次模拟,生成地表反射率(SR)数据。SR数据已经过辐射定标、大气校正等处理,最大限度地消除了大气散射、吸收、反射引起的误差。Sentinel-2MSIlevel-2a数据集为经过处理后的大气底层反射影像,时间分辨率5d,共7个波段,其中4个可见光及1个近红外波段的空间分辨率为10m,短波红外和1个红边波段的空间分辨率为20m
三、以训练样本为依据的波段选择
根据是否依靠样本先验信息,将高光谱图像波段选择分为监督波段选择和非监督波段选择。监督波段选择利用标记的训练样本参与波段选择过程,使得选出的波段子集具有较好的实际应用性能。但因训练样本需要进行实地调查,其获得的成本高,耗时费力,有时甚至无法获得,使得监督波段选择的使用受限。非监督波段选择不需要除影像本身之外的其他先验性的训练样本信息,只根据影像本身的特点进行选择,在样本难以获得的情况下更具实用性。由于没有标记样本而无法获得高光谱图像的准确信息,非监督波段选择一般以波段信息量和波段间的相关性为准则来进行选择。同时,这些波段容易受到噪声或者异常的影响,往往具有较低的鲁棒性和可靠性。此外,非监督波段选择技术一般并不针对特定的应用,因此选择的波段子集的实际应用效果较有监督选择的波段子集差。
四、以与应用模型的关系为依据的波段选择
依据波段选择与应用模型学习算法的关系,高光谱遥感图像的波段选择分为:
(1)过滤式波段选择,该方法先按评价指标对高光谱数据进行波段搜索,然后再训练模型学习器,波段选择过程与应用模型的学习算法无关,二者之间相互独立。这种方法相当于先用波段选择过程对数据进行“过滤”,再用过滤后的特征来训练模型,特点是计算量小,速度快,但波段选择结果与应用模型所需性能偏差较大。
(2)封装式波段选择,该方法将应用模型的建立与波段搜索的过程结合起来,利用模型学习算法的训练准确率作为波段子集的评价准则,因而应用模型性能精度较高,波段选择结果偏差小,但每次波段子集评价都需要重新训练学习器,运算复杂度高,计算开销大,不适用于大规模数据集。
(3)嵌入式波段选择,该方法在应用模型学习器的训练过程中通过优化目标函数自动完成波段选择。其性能介于过滤式和封装式法之间,相对于封装式法,嵌入式法避免了评估每一个波段子集对学习器进行的重复训练;相对于过滤式法,嵌入式法的波段选择结果与应用模型适应性更好。但嵌入式法性能的优劣依赖于参数调整,且目标函数构造较困难。

为什么需要波段选择?波段选择与特征提取(波段提取)的区别?
高光谱波段之间具有很高的相关性,无论在定量遥感应用,还是属于地物分类的应用中,都会考虑利用其中的有代表性的波段作为"特征波段",一是较少运算量,二是剔除对研究没有啥用的波段,其中涉及到的技术手段主要有波段提取和波段选择,波段提取是利用线性或非线性的方式对原始高维波段进行变换,达到降维的目的,其“特征波段”中的信息是原始所有数据信息的综合,而特征选择,是在原始的高维波段中,通过某些准则或方式在原始波段中选择出若干个波段,强调的是在原始波段中通过什么方式进行选择。相对与波段提取技术,波段选择具有以下优势(提取和选择各有优势,在此描述的是波段选择,所以将其优点描述一下,具体目的具体讨论)
1. 从原始数据选择出的波段,没有进行相关的其他处理,依旧保持波段代表的物理意义,在一些定量遥感应用中(如植被参数反演和水质参数反演等),保留波段的物理意义极为重要;
2. 多光谱传感器波段设置。多光谱遥感只对一些特定的波段进行成像,与高光谱数据相比,具有数据量低、空间分辨率高等特点。很多多光谱传感器只针对某种特殊应用,这种情况下,一些特定波段就可以解决问题,而波段的设置是十分关键的问题。通过对高光谱图像波段选择,可以模拟得到这些关键的波段。不仅如此,这些波段组合在应用中的效果还可以得到可靠的评估。反观特征提取,由于得到的特征失去了物理意义,对波段设置难以提供有价值的参考;
3. 物性的理解。一般而言,不同的物质在光谱上会有不同的表现,但也可能由于光谱分辨率及光谱范围的限制表现为异物同谱。在数百个波段中,往往只有少数波段在地物彼此区分中起到了关键作用。通过波段选择,可以找到这些特定波段,从而提高对物体性质的认识。
明确问题之后,进一步地需要了解什么是波段选择,怎么选择?涉及到哪些具体问题?
波段选择的问题就是在原始波段中选择哪些波段作为“特征波段”,其中必然涉及两个问题,一是为什么选择这些波段,二是怎么选择这些波段,对应的分别是波段选择的评价以及波段选择的方式。
1. 波段选择评价方式是指针对一个选择出的波段子集,给出一个定量的指标用来评价该子集的性能优劣,指标常称代价函数,目标函数或准则函数等,常用的评价指标有信息量(方差)、信息散度、相似性和独立性等。还有一些方法使用应用效果对波段子集进行评价,这类方法一般为监督方式,需要一定的训练样本。使用这种方法时,对于一个特定波段子集,首先将它们带入应用场景,并将得到的应用效果作为性能优劣的评价。例如,一些方法直接使用分类精度作为波段子集评价指标。一个好的波段子集评价指标应具有应用效果好、鲁棒性强及易于计算等特点;
2.波段子集搜索策略是一个组合优化问题,即利用评价方式对波段组合(波段子集)进行评价后,利用搜索策略从中搜索出满足条件的波段组合(波段子集)。有的方法利用评价方式后,对波段进行排序,根据排序结果选择波段子集,而不用搜索策略,具体问题具体对待,一般是用评价方法+搜索策略的方法来完成波段选择的目的。
在具体的研究领域和应用场景中,进一步的可以将波段选择问题分为监督波段选择和非监督波段选择两类,
非监督波段选择技术:指不需要除影像本身之外的其他先验性的训练样本信息,只根据影像本身的特点进行,目前主要有两种方法:
1. 基于波段排序的波段选择(往往没有考虑相关性):一般定义某种单波段指标如信息熵(InformationEntropy)、信噪比(Signal-to-Noise-Ratio,SNR)及信息散度(Information Divergence,ID)等。如最大方差主成分分析(MaximumVariance Principal Component Analysis,MVPCA)以主成分变换的基向量和对应方向的信息量加权和的方式计算各个波段的信息量,然后按照该信息量排序,波段的优先次序决定了重要程度;
2. 考虑了相关性的波段选择方法:这些方法的一个共同特点是使用针对多波段的指标。如最佳指数(Optimal Index Factor,OIF)法采用三个波段的方差和与它们的相关系数和之比来衡量波段的重要程度。然而当选择的波段较多时,该方法需要反复计算多个波段之间的OIF,这样的计算对于高光谱图像来说几乎是难以完成的。
监督波段选择:非监督波段选择技术一般并不针对特定的应用,因此往往难以获得较好的应用效果。监督波段选择技术除了高光谱图像本身,还需要提供一定的训练样本或者目标等先验信息作为波段选择的辅助信息。与非监督的主要区别在于,其评价方式应用到具体的研究目的中了,如分类中使用分类精度作为评价指标来进行波段选择,而这类评价指标的计算过程是需要先验知识作为辅助信息。
目前,对高光谱数据进行波段选择的目的应用在分类相关的领域比较多,在反演领域较少。其常用的的评价方式/指标有:
方差
在某种程度上,方差可以表示所有数据相对于平均值的离散程度,在图像中它表示 某个像元的灰度与平均值的差异水平。方差越大,其偏离均值越大,图像所携带的信息 量越多,其灰度层次也就越丰富,图像的质量越好;
熵与联合熵
香农(Shannon)于1948年第一次提出了用熵来表征信息量,并指出熵和信号值出现的概率有一定的联系。信息熵的大小直接影响图像的质量,图像的质量随熵值的增大而变优,信息量也随之增加。由于熵可以用来表示图像所含信息量的多少,因此可以用多个波段的联合熵衡 量其所携带信息量的丰富程度。首先,找出全部可能的波段组合,并求出联合熵,然后 对其排序,使其满足从大到小的规律,从而选出联合熵最大的排名靠前的几个的波段组合作为最佳组合。若选择三个波段的组合作为最优波段,则其联合熵的表达公式 如下:
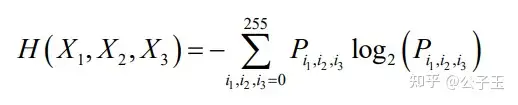
其中, 表示图像 X1 中像素灰度为 、图像 X2 中同名像素灰度为 、图像 X3 中 同名像素为 的联合概率。联合熵越大则波段组合携带的信息量越丰富,因而最佳波段 的选择问题得以解决。
OIF(最佳指数法)
对于高光谱图像的数据而言,波段的信息冗余度与相关系数有关,而信息量与标准差有关,且均为正相关关系。Chavez 等人在 1982 年提出最佳指数因子这一概念,作为 一种组合波段的选优算法,其选择的波段数目 n 通常取 3,即将全部可能的三个波段进行组合。如果组合波段有 n 个,则它们的最佳指数因子可以用 如下公式表示
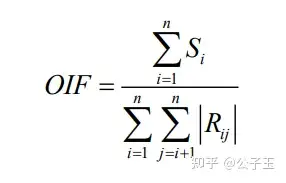
其中, 表示第 i 个波段的标准差, 表示 i j , 两波段的相关系数且要取绝对值, 通常取 n= 3。对含有 L 个波段的图像数据,先计算其相关系数矩阵,再找出全部可能的 三组合波段,并分别计算其相应的最佳指数因子,然后将其按照从大到小依次排序,则 可以选出最优的组合方案。
基于类间可分性的波段选择方法
对高光谱图像进行分类时,需要进行高光谱各波段与地物间的可分离性进行研究,一般地,地物的类间可分性可以针对单波段也可以针对多波段组合来计算,主要计算地物类别在单波段或波段组合中的统计距离,包括均值间标准差、离散度、B距离和J-M距离等,通常均值间标准差表示地物类别在单波段中的可分性,其他距离指标用于波段组合中的可分性研究。
1. 均值间标准差
其中, 分别为两类样本对应区域的光谱均值, 分别为两类样本对应的区域内的方差,d反映的是两类样本在每一个波段内的可分性大小,d越大,表明地物在此波段的可分性越好。
2.离散度
离散度是基于类条件概率之差的概念,表征了两类地物之间的可分性,其表达式为:
其中, 分别为i,j两类样本对应区域的光谱均值矢量, 分别为i,j两类样本对应区域的协方差矩阵,tr[A]为矩阵A对角线元素之和。
3.B距离
也可以化简:
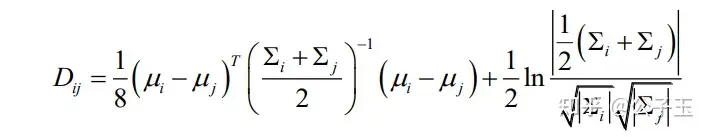
其符号意义,与离散度一样。
4. J-M距离
其中, 为B距离。 范围在[0-2],分类精度达到一定程度后不再增加,说明当J-M距离足够大时,致使分类精度已很高时,继续增大J-M距离对于分类精度的没有过多意义。
波段选择主要涉及两方面内容,一是评价准则(不论是非监督还是监督场景),二是搜索方法,此节详细描述搜索方法;
先明确一个问题,波段子集搜索(波段组合)属于优化问题,是个NP问题,没有绝对的最优子集,即最优波段组合(选择),因此,获取的解都是在一定程度上以牺牲解的精度换取搜索效率的结果,在数据量大的时候,难以用暴力搜索方式解决问题,常用的有序贯前向/后向搜索(和逐步回归的思想相似),遗传算法和粒子群算法等。
Whitney于1971年提出的,其本质上是一种“贪婪算法”,适用于多种特征子集搜索问题。SFS是一种“自下而上”的搜索算法,以波段子集搜索为例,它开始于一个波段,即首先选择使得波段选择准则函数最优的一个波段。初始化第一个波段时,需要对每一个波段各计算一次准则函数(共L次),并选择具有最优准则函数的波段。然后,在剩余的波段集合中,再次选择一个波段作为第二个波段。第二个波段选择的原则是,与第一个波段组成的“波段子集”能够获得最优的准则函数,因此选择第二个波段需要计算L-1次准则函数。以此类推,每次增加一个波段,保证能使当前的波段子集获得最优准则函数。由于使用SFS搜索,特征数逐渐增加,且每次增加一个特征,因此称为序贯前向搜索。
使用SFS从L个波段中选择n个波段子集,需要搜索的总次数为:
近似nL。
Marill于1963年提出的,其本质上也是一种“贪婪算法”,同样适用于多种特征子集搜索问题。与SFS相反,SBS是一种“自上而下”的搜索算法,以波段子集搜索为例,它开始于全部波段集合,即将全部波段集合作为初始波段集合,然后从中逐个删除波段。删除第一个波段时,需要先将每一个波段去除一次,并对剩余波段各计算一次准则函数(共L次),保留具有最优准则函数的波段子集,这就相当于去除了一个波段。然后,使用同样的方法在剩余的波段子集中,再次去除一个波段,这也需要将波段子集中的每个波段再去除一次,因此,删除第二个波段需要计算L-1次准则函数。以此类推,每次循环都保留能获得最优准则函数的波段子集。由于使用SBS搜索时,特征数逐渐减少,且每次减少一个特征,因此称为序贯后向搜索。
使用SBS从L个波段中选择n个波段子集,需要搜索的总次数为:
近似 。
值得注意的是,Pudil对序贯前向(后向)做了改进,提取了浮动的序贯前向(后向)算法,每次增加或删除的波段数不止一个,可为多个,并且对纳入子集的波段再次进行重新评估。
[1] Pudil P., Ferri F., Novovicova J., et al. Floating search methods forfeature selection with nonmonotonic criterion functions[C]. PatternRecognition,Vol. 2-Conference B, IEEE Conference on Computer Vision &Image Processing, Proceedings of the 12th IAPR International. 1994: 279-283.
[2] Pudil P., Novovičová J., Kittler J. Floating search methods in featureselection[J]. Pattern recognition letters, 1994, 15(11):1119-1125.
关于波段子集搜索方法还有智能算法,如遗传算法,模拟退火,粒子群等,正在整理中,后续附上,有时间的话,以代码的形式整理其思路,很多东西论文或其他资料中都涉及到,但大多缺乏逻辑性,缺少为什么以及细节。